Hashing and Indexing Mainframe Data

An index is a database structure, separate from the data, that provides a method to search; it provides a technique for both rapid random lookups and efficient access of ordered records. Hashing is an indexing technique that leverages mathematical techniques to organize data into easily searchable buckets.

Hash use on the Mainframe

Hashing, as a method of indexing, was made available in Db2 initially in DB2v10, and is used primarily to search for data faster than is possible using an index—in specific cases.

Hash indexing has been available in other IBM products for some time – IZTA has been leveraging indexes built using hashing techniques for years—it is an excellent complement for Db2, and can improve performance over buffered DB2 even if you’re already using hashing in Db2 and leveraging Db2’s in-memory functions.

Despite the fact that hashing has been available for some time in both Db2 and IZTA, many shops are not enjoying the benefits in speed that are possible, mostly because if it aint’t broke, don’t fix it. This article will show you how and why you should be using hashing, as well as under what conditions to use it. The result will be faster access to data, and improved performance for your transaction processing applications.

What is Hash anyway?

A Hash algorithm maps one space (typically very large, with many points) to another space (typically much smaller, with less points)—in a one-way mapping scenario—you cannot have a reverse mapping. It typically shrinks the space you’re working with, mapping a large number of points to a much smaller number of points. In terms of memory in a computing device like that mainframe, that means mapping to very specific space—an area in memory or a place in an index.

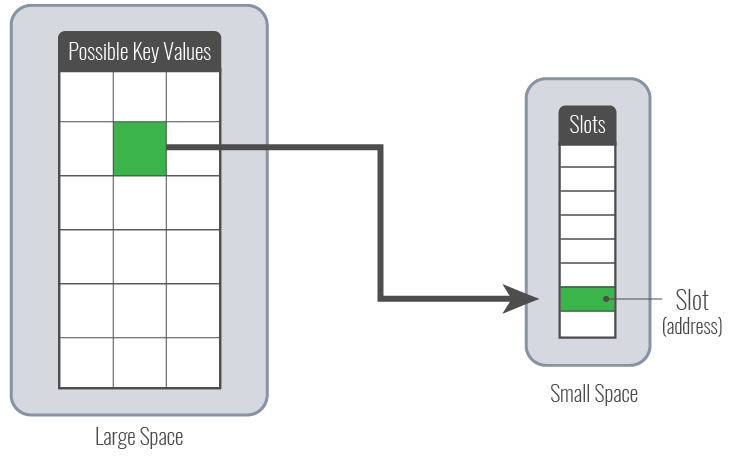
In this example, hash can be used to calculate a slot in memory—the slot calculated can be a pointer to the key in memory.

Effective hashing is a repeatable process, but there are several things to consider—folding/consuming, dividing, use of primes and collision mitigation. Encrypting passwords is another use of hash, mapping any password, to a new space. Because hashing is repeatable, the process can be used to check if an entered password is valid, etc.

Folding/Consuming: is used to deal with arbitrary length starting point. An arbitrary length variable can be mapped to a fixed length number. Broken in to blocks (normally bytes) and combined to produce a number.

The combination process normally puts a different weight on each byte, by multiplying out. Different Hash algorithms use different methods to combine the different bytes—addition, OR and XOR are all used, as well as different multiplying factors—often but not always using primes. The cost of this folding process is proportional to the number of folds and therefor the length of the item being hashed.

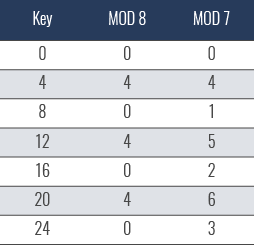
Dividing: to map to arbitrary sized space, the number from the folding is divided by the size of the space, and the remainder is the hash output (Modulo N, where N is the size of the space we are mapping to).

Use of primes: Most Hash algorithms provide a better distribution across the target space when primes are used—this is related to keys with patterns in them, where the pattern has a relationship (multiple) of one of the factors.

Handling collisions: mapping to a small space means collisions are inevitable; there are two common methods for handling this—

1. Use next available empty slot—the advantage is that you don’t need more space (the size of N); but this approach can increase collisions.
2. Use a link list containing a list of items that collide—the advantage is there will be fewer collisions; but space requirements will be unpredictable (you have to consider 100% collision rates)

Density will play a role as well—that refers to the number of slots available for the amount of elements to be stored; e.g., in a case where 100 items are to be stored, if we allocate a Hash with 500 slots, then we have a density of 20%. With higher density, the probability of a collision is greater; the lower the density, the more space is required. If collisions are being handled by next-available-slot, you must keep the density below 100%.

How does a well performing Hash behave?

A well performing Hash must have a low collision rate (independent of key type, length and distribution), and must ne easy to calculate (you want to minimize CPU cycles). So, which of those is MORE important? Well, that depends…

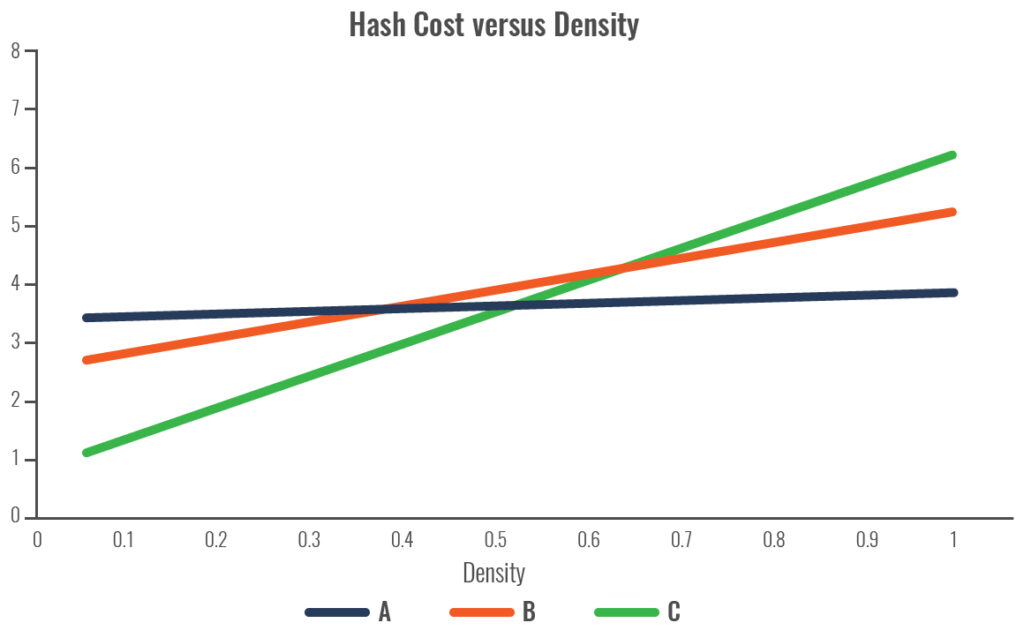
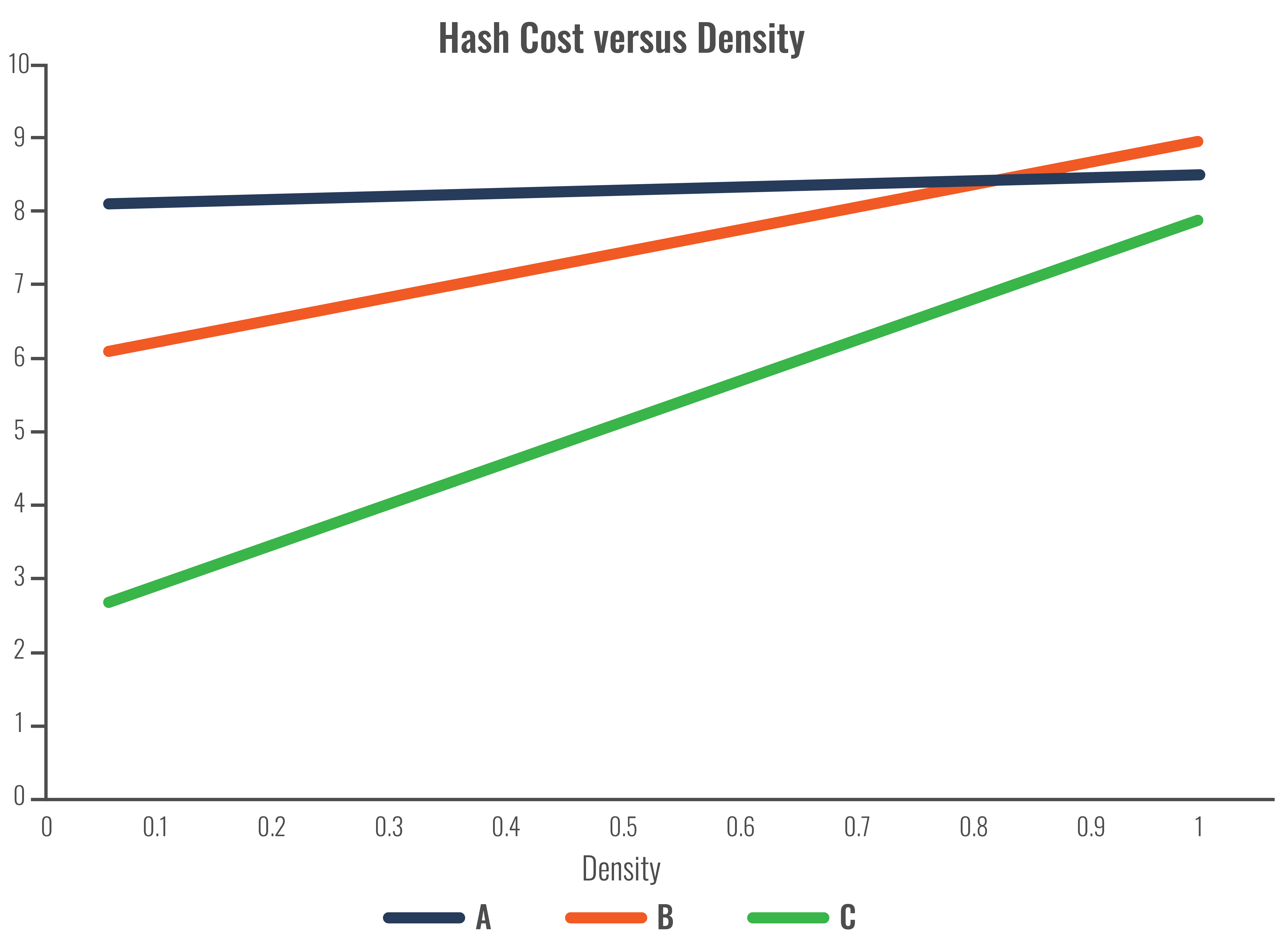
Let’s consider three hypothetical Hash algorithms with different effectiveness—the cost of handling collisions is x, and the ideal collision rate is i.

Algorithm A:

• Cost to calculate Hash is 4x
• Collision rate is i

Algorithm B:

• Cost to calculate Hash is 3x
• Collision rate is 6i

Algorithm C:

• Cost to calculate Hash is x
• Collision rate is 10i

For all three cases, we can look at the cost (CPU required) to calculate, depending on the density; the results for these three cases:

What happens if we double the key length:

What can we learn from this?

Whereas we will typically know the key length and the key type (numeric, ASCII, etc.), we may not know the number of row or the key distribution—and these all can impact the probability of collision (the higher the density, the more likely there will be a collision). As a result, more effort needs to be executed to deal with that collision—so the efficiency in computation has to be weighed against the amount of space you allocate for the index (the more space, the less likelihood of a collision).

Choosing a Hash Algorithm

The ideal hash algorithm is easy to calculate (processing power impact), low number of collisions, a good distribution to the target space, irrespective of distribution within source space. For illustration purposes, we will consider some proprietary algorithms, along with a publicly available algorithm, Fowler-Noll-Vo Hash, labelled as “F” in the following graphs.

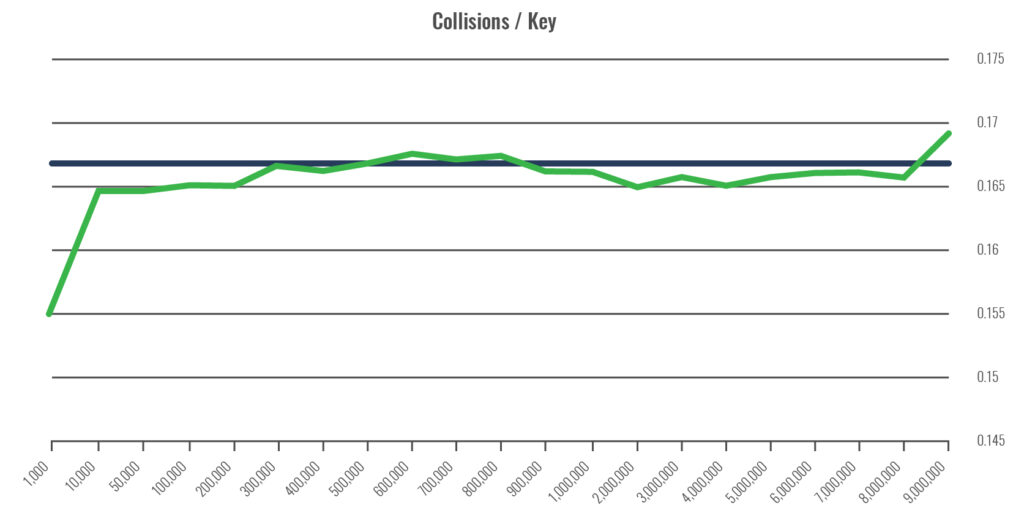
The image below shows the number of keys, or number of rows in the table (vertical), against the number of collisions divided by the number of keys. This is relevant because the number of collisions is theoretically related to the number of keys. The Purple line is the expected result based on density, the blue line the measured.

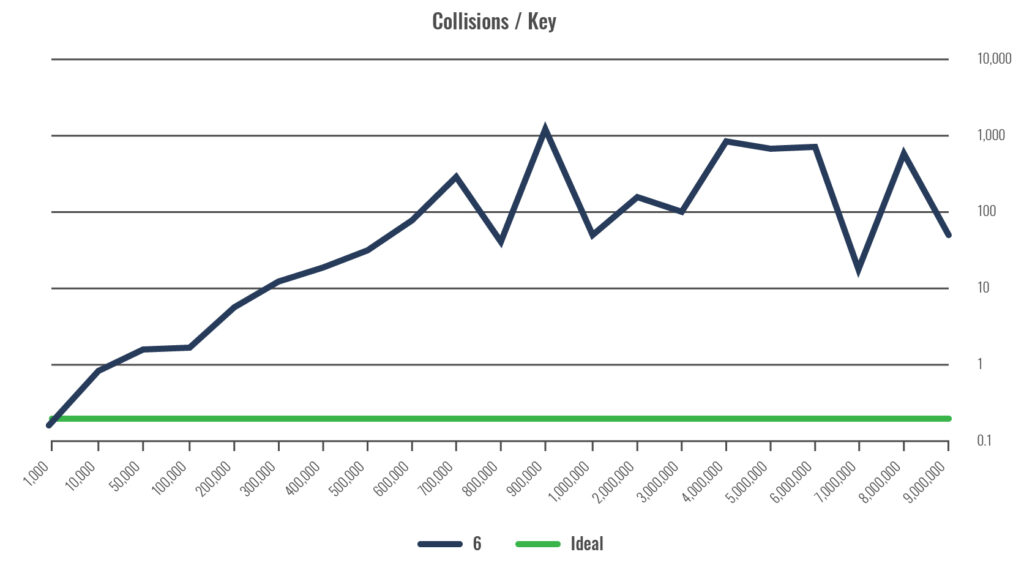
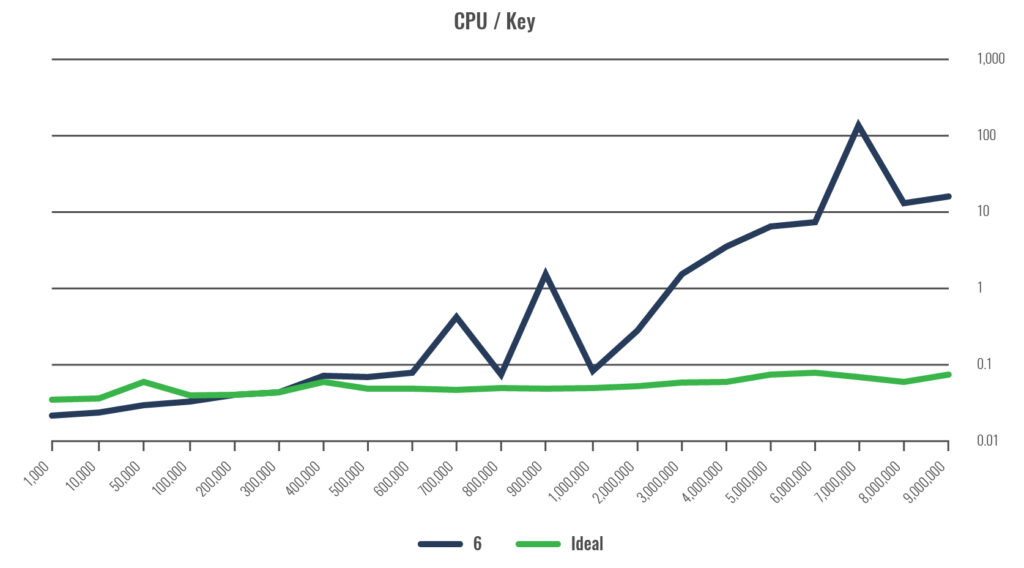
The following image is essentially the same, with the difference being that the key distribution that isn’t friendly to the hash algorithm. This one shows a proprietary algorithm (labeled as “6”), and how CPU usage is impacted – this should be considered a relative measure.

Finally, several algorithms are shown in best-case scenarios.

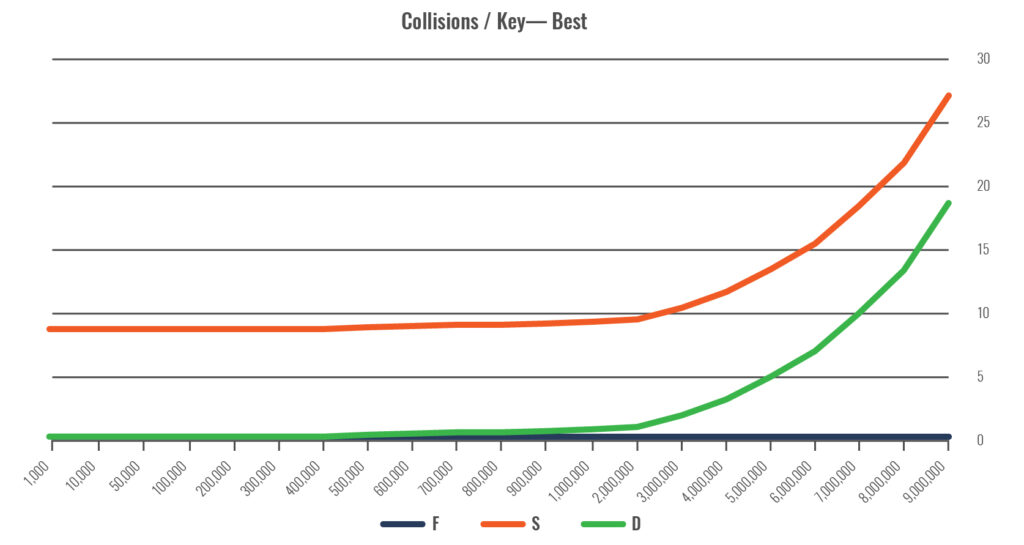
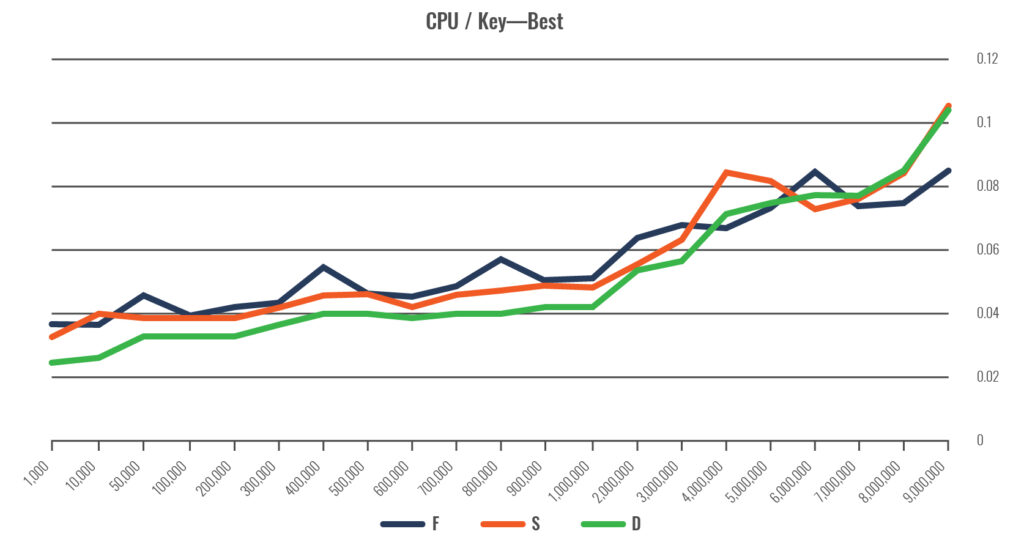
Now What?

If you don’t have enough information, it’s best to select a highly efficient Hash algorithm, like Fowler-Noll-Vo Hash Function – FNV (or “F” above). On the other hand, if you know you have well-distributed keys, a small number of keys, and very low density, you may want to consider a Hash algorithm that is cheaper to calculate.

A Cheaper Hash

An interesting example of an index distribution that could be leveraged to use a cheaper hash function is the use of alphanumeric post office codes in Canada, which are in the form of ANA-NAN. The following patterns are known: characters D, F, I, O, Q, and U are not used, while characters W and Z are not used in the first position.  The six bytes have 300,000,000,000 combinations, but you can limit the number to 7,400,000 with knowledge of distribution; further, only about 830,000 are actually in use.

Standard hash

For general non-specific uses, there are a series of standard Hash algorithms available. For example, there are Linux 32 and 64-bit Hash algorithms:

F

Where:

• p is a prime (31)
• n is the number of bytes
• b is 32 or 64

It maps any string to either 32- or 64-bit numbers. This doesn’t behave well with high densities, however, with combinations 2³² or 2⁶⁴, low densities should be guaranteed.

This method is mentioned because the algorithm is well known; it is very useful as part of a password encryption process.  However, this particular algorithm unchanged, would not be very useful as the index – as it generates such a huge number of index slots it would consume an awful lot of memory! As with all index designs, you must tailor your solution to your own specific conditions and goals.